
Powers and Exponents are a foundational skills that will continue to show themselves again and again in more advanced math, so making sure that your students master it will help them for years to come.
This one of many reasons why, when teaching this and other concepts, you want students to understand how this standard works, not just memorize a shortcut.

Discover or Teach?
Most teachers begin their lesson by explaining to their class what exponents are, how they work, and then giving them multiple examples followed by practice problems. Drill and repeat is utilized to help students memorize the rules and terminology.
While this method will work, there are some alternative methods to teaching this skill.
Discover the Rule
One such way is to give students a series of examples and ask them if they can deduce the rule.
For example, you could write the following on the board:
If 24 = 16, what does 26 = ?
If 32 = 9, and 33 = 27, what does 34 = ?
If 22 = 4, and 32 = 9, what does 62 = ?
A series of investigative questions like this well help your students think about the pattern and discover the rules.
Discovery with Increasing Complexity
For an alternative approach to the above methodology, you can have a series of these questions printed in ascending order, each one more complicated than the next.
You can write the first one on the board and put students in groups to solve it together. Peter Liljedahl, in his book Building Thinking Classrooms, would recommend this approach, and he would advise that the small groups work on whiteboards hanging on walls around the room with dry-erase markers (one per group). After a group of students correctly solves the first problem, they go get the second, and then the third, and so on.
Walking Question Gallery
Another alternative to the above teaching activity is to hang the questions on pieces of paper around the room. This is called a walking galler. As students walk to each problem, they solve them on their sheet of paper. They can do this independently or in small groups.
Split 25 – from Making Math Moments Matter
One more great discovery activity comes from MakeMathMoments.com where they recommend a game called Split 25. You can watch their explanation of the game on this video, or read my quick overview below.
In Split 25, the teacher puts a number on the board, like 25, and asks the students to come up with different numbers that when added together equal 25.
For example, 24 + 1 or 12 + 11 + 2.
After getting a few examples, the teacher writes the examples of numbers that when added together equal 25, and then the teacher multiplies those numbers instead of adding them.
So 24 + 1 becomes 24 x 1 which equals 24. And 12 + 11 + 2 becomes 12 + 11 + 2 which equals 264.
The teacher then asks the class to work in groups to come up with the largest product possible using numbers that add up to 25.
Quickly, students will see that the more numbers in the solution, the better their chances of a big number. Eventually, you will have students doing 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 1 or something similar.
As students write these reoccurring small numbers being multiplied repeatedly, the teacher will help them with the shorthand. Showing them that 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 can more efficiently be written as 211.
What I love about this activity is it gets the students competing, so there is an element of fun, and they are still discovering the rule and how it works.
An Important Concept to Grasp
While teaching about powers and exponents, it’s importnat thta your students understand that an exponent is a way to abbreviate repeated multiplication.
Just like multiplication is repeated addition, exponents are repeated multiplication.

Some teachers like to show the students this problem:
2 + 2 + 2 + 2
And ask them a shorter way to write it.
Hopefully, your students will know that 2 + 2 + 2 + 2 is the same as 2 x 4.
In the same way that the multiplication symbol denotes repeated addition, the exponent denotes repeated multiplication. Instead of writing 2 x 2 x 2 x 2, we can write 24.
Terminology
Another key component to teaching powers and exponents is focusing on vocabulary. There are several key terms that students need to know. The big four are:
- Exponent – the number of times the number is multiplied by itself
- Base – The number that is being multiplied by itself
- Power – raising a base by a power
- Expanded Form – the power represented by the base being multiplied by itself repeatedly
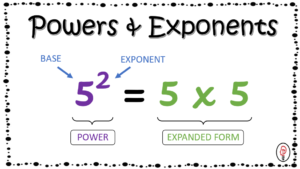
Here is an image that you can use for your word wall. It’s a free download below. I recommend using the black and white version I will send you and having your students color it in. It goes great in their notebook or to hang on the wall. You can also use it as part of your learning station or center.
Practice with Feedback
After introducing the topic through discovery or tutorial, it is important to give students lots of practice with immediate feedback. Immediate feedback means that you let students know whether they got the answer right or wrong immediately after they complete each question.
This is very hard to do when you are using whole group instruction because many students work at a faster pace than others. Here’s what I do.
I put one problem on the board, it should not be complicated. For example: 7 x 7 x 7 x 7 x 7 x 7
I allow the whole class about 20 seconds to try to solve. It’s important not to give your class too much time. Obviously, part of the difficulty of this task is trying not to miscount the number of terms on the board – so if you have a textbook or worksheet and tell everyone to do #1 only, this is also effective since the students will have the paper in front of them and they can use their pencil to count the number of terms and help with their tracking.
After a short period of time, usually 20 seconds, as mentioned abovve, I give the solution; 76.
I then give one short problem of the inverse, where students are given the exponent and asked to write the solution in expanded form: 54
Then, I do a second round, this time I assign two more problems just like the previous one, not increasing in complexity.
5 x 5 x 5 and 2 x 2 x 2 x 2 x 2
I again ask everyone to solve on their own sheet of paper and I give them a very short period of time before providing the solutions.
Then, I assign two problems where students need to write the solution in expanded form when given a number with an exponent.
13 and 92
Finally, I do a third round of questions, this time a bit trickier. I put 4-6 problems on the board, half where students write the expanded form and half where students write the exponent, but this time I utilize variables for the base, I use the number 1 for the exponent, I throw in one problem with two different bases, and I use different ways to write the multiplication symbol – parenthesis and dots.
This will be the most tricky part because many of your students will not try, and they will say things like, “you didn’t teach us this,” “I don’t know what to do,” or “I don’t get it.”
The trick is to try to get them to engage in productive struggle.

The Importance of Other Multiplication Symbols
For numbers 9 and 11 above you will notice that I use symbols for multiplication besides “x”. It is important to begin to expose your students to this and exponents is the perfect place to do so (if you have not already).
I strongly recommend you ask students why we don’t use an “x” for numbers 9 and 11 above. The answer, of course, is that the “x” would be confusing since there are variables in the problem, and the multiplication symbol could be mistaken for the letter x. So as mathematicians, we use a floating dot or parenthesis. Later, you can let them know that there will be nothing for multiplication – just a number touching a variable, like 8s or 14x.
How to Get them to Engage in Productive Struggle
I have several different strategies to try and encourage productive struggle. I usually introduce the idea of productive struggle to the class before they see the difficult problems. I’ll say something like, “I’m going to show you some problems that you don’t yet know how to solve. But I want you to try. I bet you can figure them out. I do not want you to raise your hand and ask for help and I do not want you to give up and quit. I want everyone to try. Remember, there’s no penalty for getting the wrong answer.
Another good strategy is to walk around the room and give positive feedback. “I really like how Angela is making an effort.” “Looks like Pierre has gotten one of the questions right.” “I like how Juan is trying his best. He’s not giving up and he’s not asking anyone for help.”
Productive struggle is very hard. Students are not used to it in the traditional classroom environment where everything is drill and repeat. Plus, as humans, we are wired to conserve energy by taking short cuts. So it’s natural for students to want to shortcut the process by asking a friend, asking you, or just waiting for the solution. So try not to get frustrated, but do try to motivate and challenge your students to persevere.
For more about encouraging your students to participate in productive struggle, click here.
Another Tip
One more strategy I like to implement in round 3 is to have the answers ready for my students. So when they finish each problem, they can check their answers. I have different ways to do this. Sometimes I have index cards with the problem number on one side and the solution on the back that I pass out or put in envelopes. Sometimes I put the answers to each question in different areas of the room and students are encouraged to go check their work when finished. Another strategy is to have them work in groups and give one person the answer sheet, they are responsible for checking the groups work after the group has decided on an answer.
Whatever your methodology, give your students immediate feedback. It is not easy to do by yourself (with you circulating and telling each student if they got it write or not), so think through some alternative ways.
Guided Notes Worksheet

This guided notes worksheet is a free download in my TpT store, or you can click here to get all the free resources from this article.
Independent Feedback
The above questions have set your students up for the majority of problems they will see.
I would encourage you to have your students write down all the practice problems in their notebook, journal, or whatever you are having them take notes on so that they can reference it as they do their independent work. You can get guided notes and other printouts for their journals here.
After reviewing these practice problems, it’s time for your students to start practicing the skill repeatedly with immediate feedback. Remember, we do not learn through practice we learn through perfect practice. This means that it is not enough to give your students 20 practice problems, you must make sure that they are given immediate feedback on each question so that they know whether or not they are doing the work correctly. If they are, they can gain confidence as they proceed. If they are not doing the work correctly, they can learn from their mistakes. This is why they must be given feedback on each question.
To give immediate feedback you can have students work on technology – like Khan Academy, AAAmath, or IXL – which provides feedback after each question. OR, you can use one of the strategies I mentioned above with answer sheets, answer cards, etc. However you choose to provide feedback, please do so.
One more note on immediate feedback. If you are giving students answer sheets, stress to them the importance of making an attempt before checking to see if they got it right or not. We know that there is a natural tendency to cheat, and just write down the answers that have been given to you. Especially in this type of problem where there is no work to show. So help remind them of the correct process so that they don’t make this error, which would be detrimental to their learning.
Exponents Worksheets and In Class Activities
For more worksheets to give your students check out these resources:
Reteach Worksheets
To help your students work independently, discovering how to do the work – or to use as whole class guided instruction

Color by Numbers Worksheet
Students answer powers and exponents problems which tells them which color to shade in each box, resulting in the correct image. Lots of fun. Also great for your sub folder.

Maze Worksheets
Another great extension activity. Students solve problems to correctly navigate the maze. Only by solving problems correctly will they reach the finish line. Excellent way to get immediate feedback.

Cut and Paste – Matching Activity

Bundle: Learning Station Resource Pack
All of the resources mentioned in this post are available as one purchase, which includes more practice worksheets, quizzes, pennants to celebrate success, and more. Click here to purchase


