
in 5 Easy Steps
Scientific notation—a relatively straightforward process that so many students struggle with. Why? There may be many reasons, but I think it’s partly because many math teachers are strapped for valuable class time, and they tend to rush over it.
But there’s a way you can help your students master converting scientific notation into standard numbers, converting standard numbers into scientific notation, and performing operations with numbers expressed in scientific notation – without spending days and days covering it. We’re going to discuss how to these 8th grade math skills in the simplest, fastest way, all while keeping students engaged.
1. Lay the Foundation
Before you jump in, make sure your students have all the tools they need to learn scientific notation. Spend some time reviewing Place Value, Exponents, and terms like “to the power of.”
Without these foundations, students will needlessly struggle with scientific notation. Check out these worksheets that can help you review:
- Add, subtract, multiply, and divide numbers with decimals
- Exponent Rules: Multiply, Divide, and Power of a Power
- Powers and Exponents
- Negative and Zero Exponents
2. Explain the “What”
Part of the reason many students struggle with scientific notation is that they don’t understand its purpose or value. When students don’t see the value in what they’re learning, they tune it out, and their grades reflect it.
What is the what?
Basically, scientific notation is a type of shorthand. We use different forms of shorthand every day—abbreviations, symbols, and even emojis can represent words in a shorter form.
Consider asking your students what texting abbreviations they frequently use. (LOL, SMH, FR, WYD, WDYM come to mind.) Just like we use abbreviations through text, we also use scientific notation to make big or small numbers easy to write and understand.
In short, scientific notation is a method of presenting very large numbers or very small numbers in a simpler form.
Give the example of pi—a number your students should be familiar with. You can’t write out all the numbers of pi on a sheet of paper, or even every sheet of paper on planet earth. So what do we do? We create a shorthand.
Instead of writing all the numbers of pi, an impossible task anyway, we use the Greek π symbol. But not every number in the universe can have its own fancy symbol, so we use scientific notation for the rest.
3. Explain the “Why”
First and foremost, mathematicians are lazy. To their credit, scientists are also lazy. Students are lazy, and teachers are lazy, too. In fact, all humans are lazy because we will never do more work than we need to. That’s why, when presented with numbers that have a lot of digits, we want to shorten them as much as possible, to make it easier to read and write.
Show your students a really long number on the board, such as the mass of the earth. Scientists estimate the mass of the earth to be 6,000,000,000,000,000,000,000,000kg.
Have your students imagine this scenario: their cruel math teacher has decided that students will write essays on their math lessons. Today they will write a 1000-word essay on the mass of the earth. Throughout this essay, they will inevitably have to write the number over and over and over again. They will probably get hand cramps writing all those zeros.
Using scientific notation, however, they can convert this number into a much simpler form to represent the earth’s mass: 6 × 1023.
Ask students to theorize other extremely large numbers, or small numbers, that would be difficult to write – so writing them in scientific notation would be much easier.
Examples of numbers that need to be written in scientific notation:
- the weight of a planet
- the weight of an atom
- the distance from our planet to another galaxy
- the length of a microscopic deep sea creature
- how far Superman could travel if he ran as fast as he could for an hour
4. Explain the “How”
Decimal notation to Scientific Notation
The “regular” version of these long numbers is called decimal notation, as opposed to the shortened scientific notation.
Show your students that scientific notation will always follow a specific format: __ × 10n.
When converting to scientific notation, the goal, essentially, is to determine the value of the exponent. To achieve this goal, all we really have to do is count. And tell your students it’s basically that simple.
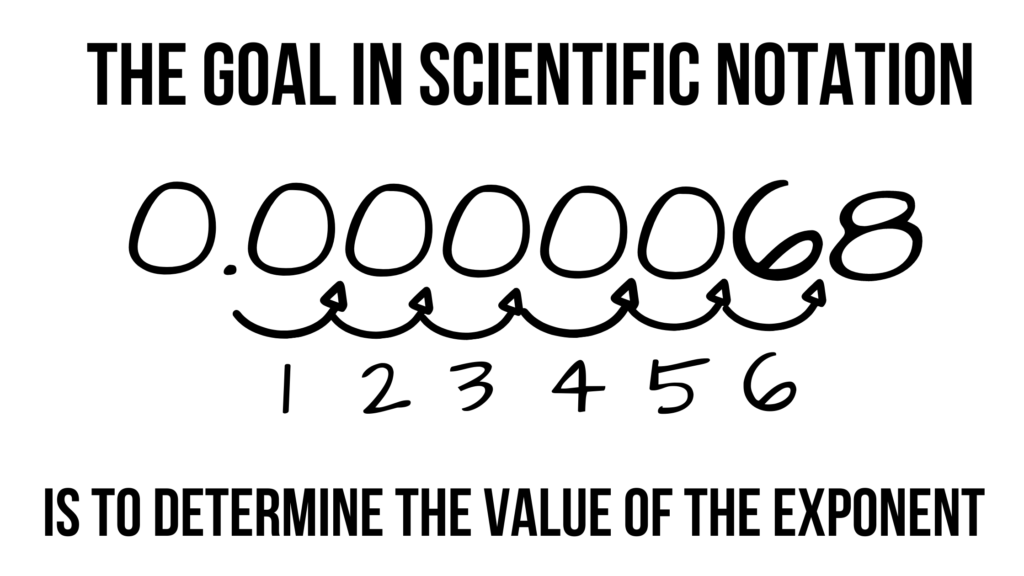
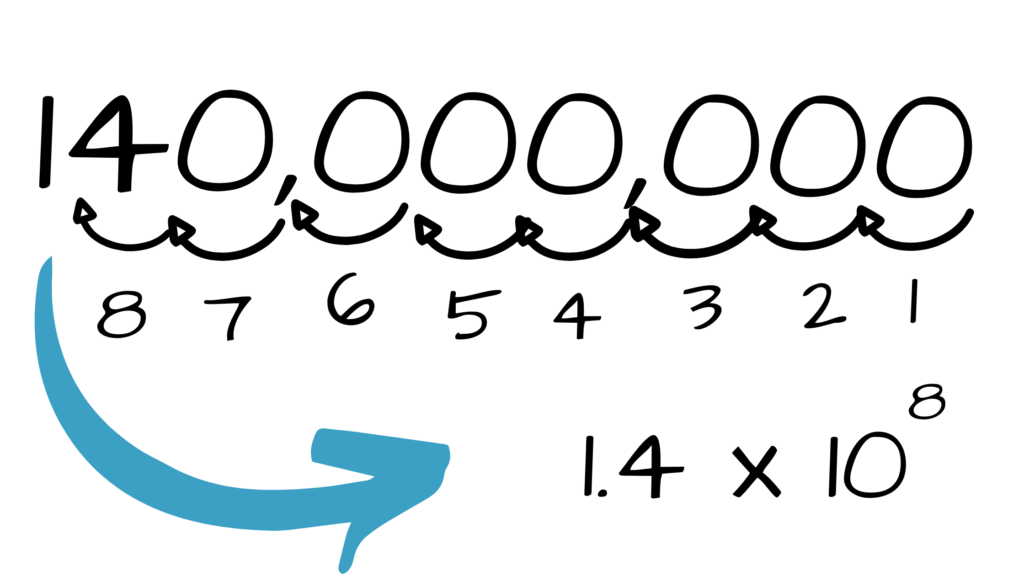
Let’s work with another big number. The surface area of all the water on earth is estimated at 140,000,000 square miles. To convert this number to scientific notation, have your students follow these simple steps (you may want them to write these steps down, or have them repeat the steps after you):
1. Locate the decimal.
For some numbers, the decimal may not be written but is understood to be at the end. So for the surface area, we can assume the decimal falls at the end as well (140,000,000.0). For very small numbers (less than 1), the decimal will already be written.
2. Move the decimal.
The reason we want to move the decimal is to get rid of all those pesky zeros. But we aren’t moving the decimal just any ol’ place—we have to move it to the perfect location. Always move the decimal after the first digit that is not a zero. In the surface area example, that would be after the 1 (1.400000000). Remind your students that for very large numbers, the decimal moves left, and the exponent will be positive.
Please Note: It might also be beneficial to explain to your students that when they move the decimal, and get rid of all the zero’s, the new number will be a number greater than one but less than 10.
3. Count the moves.
As they move the decimal, your students should keep track of how many decimal places they moved it. In essence, our notation is starting at 100. The number of decimal places it moves will become our new exponent.
When you count the “moves” in 140,000,000, have your class count along, saying “ten to the first, ten to the second, ten to the third, ten to the fourth” and so on. Counting aloud helps students recognize how moving the decimal affects the exponent.
If your students struggle with Place Value, they might struggle here. Consider asking your students how many decimal points it would have to move to fall just behind the 1. This may help you identify if you need further review before moving on.
You can explain that moving the decimal is like taking it on a road trip, and you need to keep track of all its stops along the way.
4. Write the notation
The rest is simple. Once they have moved the decimal, they will write the new number without its zeroes. Always follow this simple pattern:
__ × 10x
Since they already have their new number, and since they should have already counted how many place values the decimal moved, they have all the components they need to fill in the rest:
1.4 × 108
When working through the first couple of examples, say the steps aloud each time, having your students repeat after you. When working on later examples, ask students for the next steps. If they memorize the steps, they will be more likely to replicate it on their own.
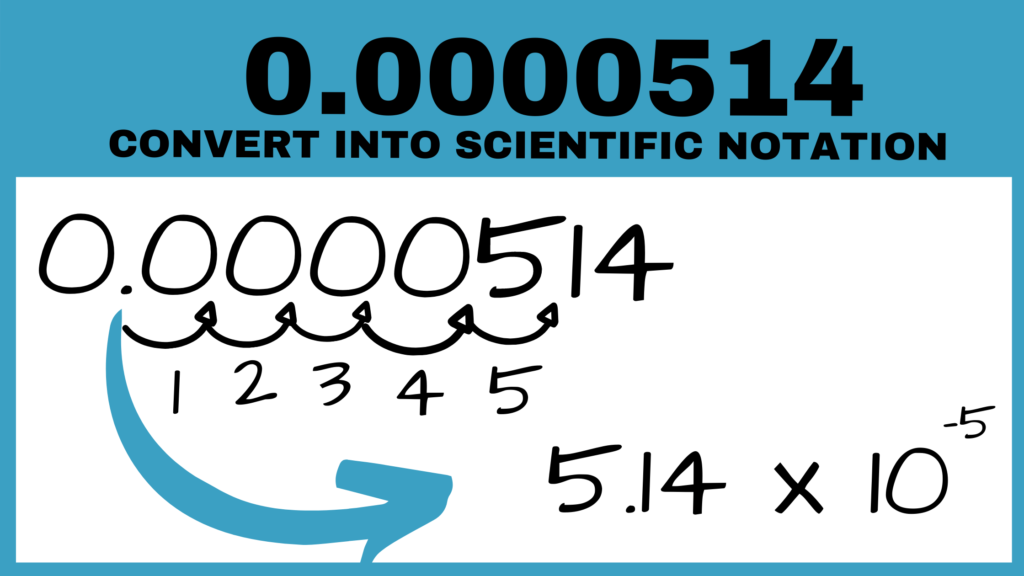
Since they now have the foundations for large numbers, go through an example with a small number. When working on very small numbers, explain to students that they will move the decimal to the right. As a result, the exponent with be negative.
Make sure to emphasize that when you move the decimal of a large number, it will always move left, and the exponent will be positive. When you move the decimal of a small number, it will always move right and the exponent will be negative. (Left, positive; right, negative)
Scientific Notation to Decimal Notation
Once students understand the first process—converting standard notation into scientific notation—the reverse is much easier. And we’re going to follow a similar process, but the goal here is a little different. When converting back to standard notation, our goal now is to bring the value of the exponent down to zero, rather than looking for the value of the exponent.
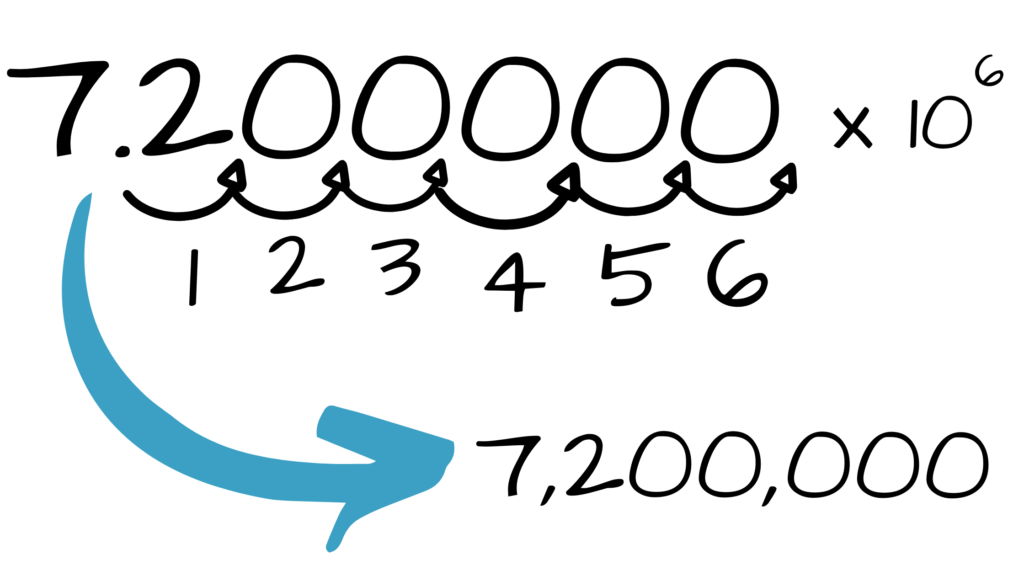
Let’s try the following: 7.2 × 106
- Move the decimal.
Before, we had a designated place to put the decimal—after the first digit that is not a zero. Now, however, we don’t have a designated location for the decimal. We have to use information in the notation to find the new perfect location. That’s what the exponent is for.
The value of the exponent equals how many place values your decimal will move. If the exponent is positive, it will now move right. If the exponent is negative, it will now move left. Remind your students this is the opposite of the first process.
Again, the goal is to get the 10 down to a power of 0. So we’re going to have to move the decimal 6 place values to get down to 0.
- Bring back the zeros.
As you begin to move the decimal, you will quickly run out of digits. To solve this problem, you will add a 0 for each place value you pass. In such a case, 7.2 × 106 will become 7,200,000.
5. Practice, Practice, Practice
The only way to master this process is to practice. Practice a few examples together as a class to build the foundation, having them repeat the steps as you go along. Then begin to ask students for the steps on their own, either as a class or cold call individually.
Once they display understanding, have them work on a question alone. You can have them work on a question individually at their desks, bring several volunteers to work on a question at the board, or ask a volunteer to go through the whole process in front of the class while the rest follow along.
However, my favorite strategy is to use learning stations to have students practice the skill we are working on. This allows me to provide immediate feedback to all of my students, and allows me to differentiate. My struggling students are given more time with immediate feedback, while my stronger students, who demonstrated mastery quicker than the rest of the class, are allowed to move on to more complicated skills (like solving operation problems on numbers in scientific notation).
Save time with the best resources.
The best way for students to master scientific notation is to practice the skill and get immediate feedback. But creating worksheets (and their answer keys!) can take a lot of time—something most math teachers don’t have.
Luckily for you, I have a plethora of resources of vetted, student-approved worksheets, including my own Scientific Notation Bundle. The bundle includes fact-based practice problems, quizzes with answer sheets, mazes, matching activities, student progress sheets, video tutorial links, and a whole lot more.
You can use this bundle to create learning stations and have students practice these principles in class, or you can easily distribute them to students working remotely. However you use them, be sure to leave a reply letting me know how they worked for you and your class.
Until then, happy teaching!




