
To help students discover the rules for positive and negative exponents, I lead the class on this one learning activity. It generally takes about ten minutes, and by the end, students will have correctly deduced both the negative and zero exponent rules.
I like to introduce the main rules for negative and zero exponents through a simple, whole class investigation.
I write 102 = _____ on the board. Even in my lowest classes, usually all of the students know that the answer is 100.
I then write 103 = _____. Even though not all of the students know the answer, several do and will tell me that it is 1,000. I normally stop and show the students that 103 = 10 x 10 x 10, and we walk through that process for just a moment.
I then write 104 = _____. By now, students are starting to get the pattern, and the whole class can help me with the next few answers.
The board now looks like this:
102 = 100
103 = 1,000
104 = 10,000
105 = 100,000
106 = 1,000,000
I then stop and ask the class to describe the pattern. Now would actually be a good time to have students turn and talk to their peers about the pattern, or even put pen to paper to articulate what they are observing.
Then, above 102 = 100, I write 101 = _____, and ask the class to think about what the answer is. Most of them, using deductive reasoning, can work the pattern backwards and conclude that the solution is 10.
We then spend a moment discussing what the first power represents, which is that number alone, not multiplied by anything. If 103 = 10 x 10 x 10, and 102 = 10 x 10, then 101 = 10. And we make a note that anything to the first power is that number.
RULE: x1 = x
If you have your students keep a notebook with notes, they should record this rule.
Then, above the 101 = 10, I write 100 = _____. Again, following the pattern, most of the students can conclude that the answer is 1. Again, we review the rule for a number raised to the zero power, and if we are keeping notes in our notebook, this is a note we should record. Or we can add it to our word wall if that is something we are doing.
RULE: x0 = 1
Understanding why a number raised to the zero power is always one is a difficult concept to grasp. I find that it’s easier to understand once we’ve learned the rules for multiplying and dividing powers. So for now, I don’t spend time trying to explain this rule. And since the pattern on the board shows them that something to the zero power is 1, the students are generally satisfied with this reason for the time being.
Now the board looks like this:
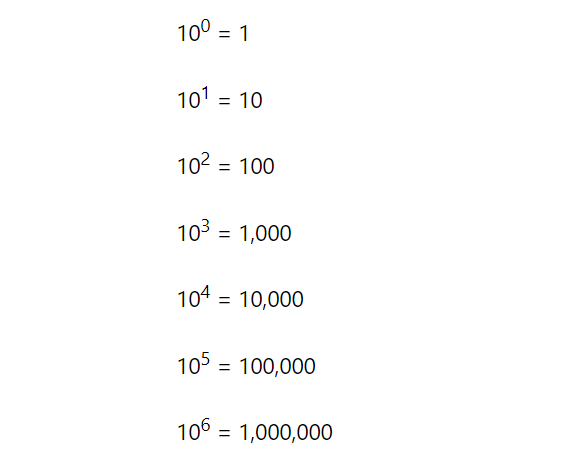
I ask the students what the next number in the pattern going up would be (above 100). This is just to review negative numbers, but the students soon realize it is 10-1. I then ask my students what this would equal, and it is not always so intuitive for our students to deduce.
But with some help, we, as a class, conclude that 10-1 = 0.1
I now repeat the pattern, going up, for a few numbers so that the board looks like this. Again, as I write each term (ten to a power) I ask students for the solution. But now that there’s a distinct pattern, they can figure out what the correct answer is.
The board now looks like this:

I then go back to 10-1 = 0.1, and ask students to read the term. “It is not ‘zero point one’,” I say. “What is the correct way to read, ‘zero point one’?” Someone will give me the answer, one tenth, and I will write 1/10 next to 0.1
I do the same with 10-2 = 0.01. I ask students to read 0.01 correctly, and they will say “one hundredth.” And will write 1/100 next to it.
Now that I have the following two equations on the board
10-2 = 0.01 = 1/100
10-1 = 0.1 = 1/10
I will ask students what similarities they see between 10-2 = 0.01 = 1/100 and 102 = 100
Eventually, they will realize that 102, with the positive exponent, has a solution of 100, and 10-2, with the negative exponent, has a solution of 100, but it is in the denominator. The same is true with 101 and 10-1 they both have a ten in the solution, but one is in the denominator.
Now we I show students that another was to write 100 is 102 so we could rewrite 1/100 as 1/102. So…
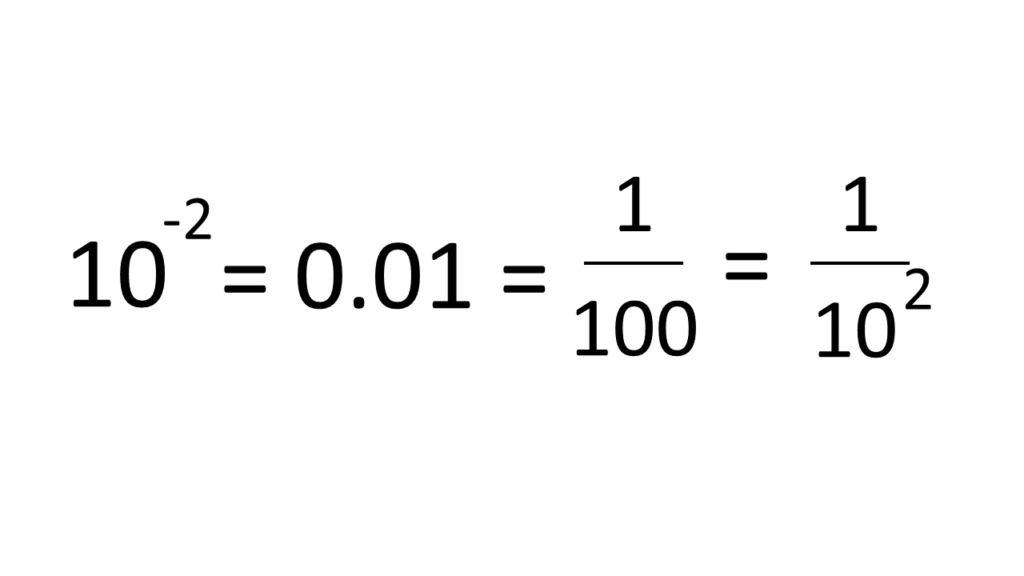
And we repeat this for all of the negative exponents in our pattern, rewriting them as a fraction with a positive exponent in the denominator.
I then ask students to think about what the rule for negative exponents is. I give them time to think independently, and then time to talk about it with a neighbor, and brainstorm together.
Then we discuss as a class, and come to the realization that
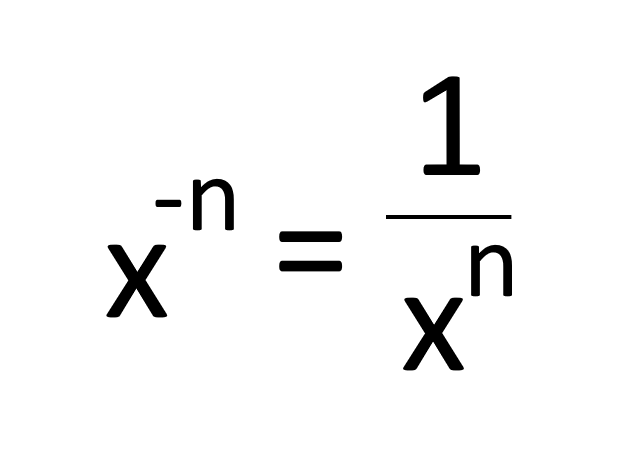
Through this one activity, we have deduced both the negative and zero exponent rules.
Making it Stick
As with all skills, for someone to learn it, they must practice it repeatedly, with immediate feedback. So after you teach these two concepts, give your students lots of practice problems on it.
Also, remember, that for practice to be effective, you must give students immediate feedback. This means that they are given the answer to every question that they complete, after they have solved it, so that they know whether or not they are doing the work correctly.
For more information on the value of immediate feedback, read this article.
Here are some great worksheets to help your students master negative and zero exponents:
Prerequisite Skills Required
The major skill that students must have mastered to be able to work with negative and zero exponents is powers and exponents. If students still have not mastered this concept, I recommend you remediate them.
Here are some resources to help you remediate powers and exponents.
Article: How to Teach Students Powers and Exponents
Here are some resources on Powers and Exponents
Exponent Rules – Reminder
Remember that negative and zero exponents are a prerequisite skill for exponent rules: product of exponents, the quotient of exponents, and power of a power.
So if your students are struggling with exponent rules, you may need to remediate them on this concept.






