
In my first years of teaching I noticed an interesting phenomenon with my students. Maybe you’ve noticed it too.
I started the unit with Adding Integers and at the end of day 1 we were all together, grasping the material. But by the end of day 2, a few stragglers had appeared. Yet, I pushed the group on.
Soon, we were subtracting integers, and I had lost several students, with a few more falling behind.
By the end of the unit, I had students all over the place: some still couldn’t add integers, some were stuck on subtracting integers, and others were lost at various points along the journey. While still others were ready to move on.
Why did things always fall apart when we started Subtracting Integers?
1) How I help my students around the issue of trying to memorize so many math rules
To subtract integers, you must convert the equation into an addition problem. Besides trying to remember to “add the inverse” (sometimes called “Keep Change Flip”), students must then remember the adding integers rules. They will also have to memorize the multiplication and division of integers rules, and many more to come.
Trying to remember all these rules, and when to apply them, can be very difficult for some students – especially for those students who already struggle with math skills.
The Problem is they struggle with memorizing the rules.
The solution is to teach number sense.
Instead of teaching a rule, and then explaining why it’s true, I like to first show the proofs to the students, and then lead them to discovering the rule.
So for subtracting integers, I like to show equivalent equations:
I would then ask the class why these two equations are the same, and then ask if this is always true. We would then test our hypothesis with several other equations. Like 6 – 1 = 6 + (-1), and 4 – 3 = 4 + (-3).
After discovering the rule, we can move forward with its application.
Too often we teach rules instead of numbers sense. Trying to remember a lot of rules is difficult, but if students understand how to figure out a rule, they are much more likely to correctly apply it.
2) What to do when you’ve spent enough time on the skill, yet some still don’t get it?
You have probably had the same struggle: I would teach adding integers (and very well might I add), yet some students still didn’t grasp the concept. So I would reteach, yet some still struggled. Despite my best efforts, there were still a group of students who couldn’t do the work, despite spending more than adequate time on it.
Inevitably, frustration with these low performers sets in, and I would progress the class to the next skill, subtracting integers. However, in so doing, I was guaranteeing that this group of students that couldn’t add integers would forever be left behind – because you can’t subtract integers, if you can’t add them.
The Problem is when you move a student on to ‘subtracting integers’ they will never master it if they don’t already understand ‘adding integers.’
The solution is to make them master adding integers, before moving onto subtracting integers.
I accomplish this by having learning stations. I have one for adding integers and another for subtracting integers, and students must show mastery in the first, before moving on to the second.
For more information on how to create your own learning station, click the image below.
3) How I make Sure Everyone Gets Enough Practice to Master the Skill
To learn a skill, you must practice it numerous times. Some people master certain skills faster than others. So some of your students will grasp Subtracting Integers quite quickly, while others will need more time.
To make sure that each student gets sufficient practice to master the skill, I load my Learning Station with lots of practice problems. I try to do this online, to give the student immediate feedback. But if technology is not possible, I have worksheets that have at least 80 questions on each – and provide answer sheets to enable students to have that immediate feedback that is necessary to learning.
The Problem is that the students aren’t getting enough practice because everyone requires varying amounts of it.
The solution is to create a learning station where everyone gets as much practice as they need.
If you do not want to create your own learning station, you can purchase all the necessary resources for $2.99 below.
4) How to Help them Learn from Their Mistakes
We all know that making mistakes is part of the learning process. Yet too often, in school, students are punished for making mistakes. This stifles creativity, and thus slows down the learning process.
How often have you (or another teacher you know) given a worksheet full of subtracting integers problems (or some other skill), and the student does all of the problems, but does them all incorrectly.
This has actually done more harm than good, because now we have reinforced a bad habit.
The problem is students aren’t learning from their mistakes because they don’t realize that they are making them
The solution is to give immediate feedback
When I give practice problems, I encourage my students to check their answers immediately. If the practice is online, like through IXL.com or KhanAcademy.org, that is done automatically. If it is a worksheet or textbook practice, I provide answer sheets, and encourage them to check their answers after each question that they complete.
Won’t they cheat? (you ask).
Well, sadly, yes. I try to encourage them not to (of course), and teach them the value of learning from their errors, etc. But in the end, there is always a student who will try to take the shortcut.
But that’s the beauty of the Learning Stations.
If they cheat on the practice problems, they won’t really learn the skill, thus they won’t pass the assessment. Then, they will have to do the learning station on subtracting integers again! Eventually, they will learn from this mistake as well (that cheating doesn’t help you learn).

5) Breaking the “I’m bad at math” complex
I taught intensive math (that’s a remedial course for students who are below grade level) at a Title 1 School (that’s a school whose students are dominantly from families of low income) for many years. I was always given the lowest students – those labeled bottom 25%.
One day I was walking my class from one building to the next and another teacher came out and started talking to my students.
“You’ll never guess what, Ms. Brown,” boasted Melina, a 7th grade student who had struggled academically her entire life. “I can solve two-step equations!” She proudly proclaimed. “Really?” responded the teacher, probably confused as to why she was even bringing this up.
“It’s true, and Brooke can solve two-step equations with variables on both sides. And Angello,” the student standing next to her, “just finished subtracting integers! So did Jillian, and Juan!” And on and on Melina went, proudly boasting about her students accomplishments.
The Problem is that students think they’re bad at math and are never shown otherwise
The solution is to celebrate their success
If you had walked into my classroom that year, you would have seen banners around the room, each labeled with one skill. And beneath each were students’ names.
As previously mentioned, my students stayed on one skill until they mastered it. And when they did, we would all clap for them, and play music, and they would put their name under the banner of that skill.
You would think that these inner city teenagers found this cheesy or embarrassing. But the truth is that they loved it! They craved it! And every day they asked me for more of it.
I had students cry telling me that they had never gotten an A before. And parents send me such nice emails after their student came home with a certificate.
And the success that they felt helped motivate them to get more of it. And because they could see their accomplishments on the wall, they started to gain confidence.
Subtracting Integers Learning Station – Resource Pack
Want more resources on Adding and Subtracting Integers?
Follow this Pinterest Board:


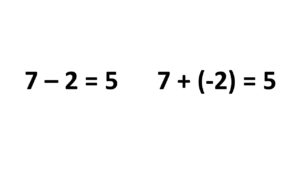






“While still others were ready to move on”?
When I was 6, I was given a spinner. I would spin it, write down the number, spin it again, write down that number, and then add the two. I could do this and get the right answer. So I continued to do it, I didn’t want to get wrong answers. Eventually I got concerned that the teacher would criticize me for not moving onto another activity. But I decided to continue until I was asked to do something else. She never did. She saw what I was doing. She saw that I could do addition. However, she reckoned that me sitting quietly practicing addition couldn’t be doing me any harm, and that I had plenty of time to do other arithmetic in my school career.
At the end of the school year she gave me the calculation 3 x 3 to solve. I didn’t know what the “x” meant. So I chose to assume that it was a badly written “+”. I returned the answer “6”, told it was wrong and sent away to do the calculation again. I returned with the answer “6” a second time, and was sent away again. So I had to guess what the questions was really asking. Perhaps it might mean three lots of three. I took the answer “9” back and told that I’d got it right. I still remember the sense of achievement I got from that event.
So what did the teacher do? She allowed me to practice, she allowed me time to get some number sense. Then she challenged me with a problem that required number sense.