
Every teacher knows the frustration of spending a sufficient amount of time teaching and reviewing a concept, only to have students still not “get” how to do the work.
I am constantly asked by my fellow math teachers the following question, “I’ve taught it over and over again, and spent more than enough time on this skill, yet several students still don’t ‘get it.’ What do I do?”
We’ve all felt that pain.
Below are 7 strategies I use that have eliminated this pain from my life. At the end of the article, I will share the easy to implement strategy that will help you do all 7 strategies at once, and effectively reach all your students.
1) It’s all About Number Sense
Math is not easy for everyone, and there are a lot of rules and formulas to memorize. Students often mix them up or struggle remembering all of them.
To help them with this, you need to teach number sense. Explain to students WHY a formula is what it is. And spend the extra time helping students make sense of it, and how to deduce it if they can’t memorize the formula.
For example, I can never remember if a number to the power of zero equals 1 or 0, so I’m sure my students struggle with it as well. So I teach this by modeling a simple thought experiment. I ask the class what 102 is. Most of them know that 102 is 10 x 10, and most know that 10 x 10 = 100. I then ask what 103 is, and guide them to the realization that it is 10 x 10 x 10, which equals 1,000. I continue asking what 10 to the next power is, and drawing the pattern on the board:
Once the pattern has been realized, I ask the students to work backwards, and simply add 101 to the top. They all realize it equals 10, and then we talk about why. We can then add 100 above that, and deduce that it is 1, simply based on the logic of the pattern.
By teaching my students it this way, I am not only teaching the skill, but I am teaching them HOW to think mathematically. Furthermore, they are being given the tools they will need to find the answer if they can’t memorize the formula.
2) Give a ReTeach, Not Another Worksheet
I am always frustrated when I observe a teacher tell their class, “you guys did really poor on this skill on the last test, so we’re going to practice it some more,” and then that teacher hands the class a worksheet.
For the record, I am guilty of doing it too.
But, honestly, this makes no sense. If the student(s) didn’t understand it on the test, why would they all of a sudden know how to do it now? Obviously there is something that they have not grasped, or are doing incorrectly, that needs fixing.
An effective way to help your students is to give a ReTeach of the skill. Again model the work, point out common mistakes, and try to teach WHY certain processes work.
3) The Secret to Committing a New Skill to Memory
When learning a new skill, you have to practice it repetitively to commit it to memory.
Yet, often, we as teachers model a problem several times, and then give the students 5 to 10 practice problems expecting the students to fully grasp the concept.
Even if they do all the practice problems correctly, if the student has not practiced the skill enough, that knowledge will be forgotten in a short period of time.
Give your students LOTS of practice. And if you have a student who is weaker mathematically, he will need more practice then most, so give it to him.
4) Practice Does NOT Make Perfect
Many times I see teachers do stations with their class, and one of the stations is a worksheet. Often, I will go over to the students in that station, and look at their work. I’m always discouraged to see students, who have done all the work, but done every problem wrong.
Practice does not make perfect. Perfect practice makes perfect
There’s no value in working many math problems, but doing everyone incorrectly. This does not help student learn, and it wastes time.
A better strategy is to give feedback after each question, so that students can recognize when they make mistakes. This also will allow them the opportunity to learn from their mistakes.
To accomplish this, I try to assign work on websites like IXL and KhanAcademy as much as possible. But if I cannot get sufficient technology in the classroom, I put answer sheets with the assigned work, so that students may go over each problem after they have attempted it.
5) Don’t Penalize Their Failures
We know that failure is part of the learning process, yet teachers often penalize students for making them, or don’t show them the error in time to help them learn from them.

Giving immediate feedback will help them recognize their mistakes so that they can learn from them. Not penalizing the student for making the mistake will give them the courage to attempt the work, so that they can learn the skill.
6) Take as Long as You Need
Many math skills build upon each other. For example, you can’t do two step equations, if you haven’t already mastered one step equations!
If a student has not mastered a skill, and then the math teacher progresses him onto the next skill, the student has no chance of mastering it.
Moving students on to more advanced skills before they are ready has not only guaranteed their failure, but it will also lead to feelings of resentment towards math, school, and you.
I give students as much practice as they need for each skill, and allow them to spend as much time as they need on that skill. Yes, sometimes that has resulted in students spending exorbitant amounts of time on one standard, and yes, they did not get exposed to all the skills that year. But I would rather my students learn three skills in one year, and master them, then me teach them 15 skills, and they learn none of them.
7) Celebrate Their Success
One of the greatest joys you will ever have is when a student has struggled, and finally “gets it.”
These should be exciting moments in their life! So make it that way.
In our class, I assess students every 4 days with a quiz on the standard that they have been working on. Which means we celebrate success every 4 days! When a student demonstrates mastery on the skill they are working on, we announce it to the class, we play music, we clap and cheer, and we put that students name under a banner that announces their success! (I also send home a certificate so they can get the same treatment from their parents).
When students can see their success, it encourages them to want to do better. It also helps them measure their accomplishments and build positive sentiments towards school and math.
Take some time to contemplate how you will measure if your student has succeeded at one of the math standards in your class, and how will you celebrate that success?

How can I Do it All in One Period?
Here’s what my class looks like:
I start with a short lesson on a standard that we are focusing on. Including exposure to test style questions and a review of their data.
We then move into our station work. Each station consists of 4 days of work on one skill that the student needs to develop (so every student may be working on a different skill). The station is built with a reteach, as well as sufficient practice to allow the student to demonstrate mastery.
The station is about 20-30 minutes each day, and it lasts for 3 days. On the fourth day, I assess them for mastery. If they have learned the skill, they move on to the next station. If they haven’t mastered it, they repeat the station until they learn the skill and demonstrate proficiency.
At the end of the period we always focus on test design, data, and word problems to help my students prepare for the assessment (the stations are to help them with the math skill).
To learn more about learning stations, you can read my book or enroll in my online course.
Click here to purchase the book, Reach Them All
Click here to Enroll in the Online Course on Learning Stations

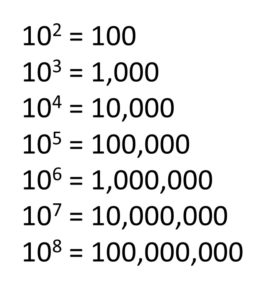


I appreciate that this general outline shows up w/ more specific examples, as I was going to respond “okay, saying ReTeach is nice but we should have options that aren’t just RePeat.” Finding a different (but not too) model to work with, something more concrete, &/or something to bridge between the concrete and symbols is a worthy challenge…